model weights contain copies: compression is not magic

part 1 of 2 • part 2: near copies and substitution

note: this post is being actively revised. citations are being expanded.

arthur c. clarke (not asimov) once famously said:

“any sufficiently advanced technology is indistinguishable from magic.”

thus it seems of late in the world of ai and copyright too. inspired by recent judicial writing, i’d like to propose a similar quote for the current age:

“any sufficiently advanced compression scheme is exempt from copyright.”

to be fair, most judges should be forgiven for their lack of familiarity with tensor products and entropy. law school selection mechanisms aside, even many with technical backgrounds have had a hard time understanding or reasoning about what we see today.

in truth, as i’ll try to convince you hereafter, it’s really not so magical. all you need to know is compressed into the list below:

• I. practically all modern generative models are trained to minimize the difference between model outputs and training data.
• II. memorization is a design choice: model capacity, training data, and optimization control the tradeoff.
• III. memorization is predictable: research shows which sequences get memorized based on duplication frequency, rarity, model size, and training decisions.
• IV. practically all models (even small, generally lossy ones) reproduce some verbatim copies of training data.
• V. reproduction requires encoding: if model weights can reliably emit a complex sequence, they must encode it in machine-recoverable form, regardless of how fancy it may seem.
• VI. therefore, under copyright law, model weights are ‘copies’—they fix content in a form that permits reproduction. if weights encode even one copyrighted work, distributing them distributes unauthorized copies.

we’ll go through each of these points below, supporting them with real evidence. by the time we’re done, i hope you’ll appreciate the following:

the question is not whether model weights can contain copies,
but which works a specific model contains.

a crucial distinction: copying vs. copyrightability

this post addresses a technical question: can model weights contain extractable copies of training data? this is separate from the legal question of whether that training data is copyrightable in the first place.

these are orthogonal concerns:

• extractable copying (what this post demonstrates): can you retrieve training data from model weights through prompting? this is about the mechanism—memorization and extraction.
• copyrightability (a separate analysis): is the training data protected by copyright? requires human authorship, minimal creativity, originality.

why this distinction matters:

1. AI-generated training data: as AI generates more content that becomes training data for future models, copyrightability boundaries blur. the US Copyright Office (2025) confirmed that purely AI-generated content without human creative contribution is not copyrightable. yet models can still memorize and extract it.

2. independent creation vs. extraction: copyright law has an independent creation defense—if two works are independently created, no infringement exists even if identical. but extraction from weights isn’t independent creation, it’s retrieval. memorization ≠ original thought.

3. compilation copyright: Feist and 17 U.S.C. §103 establish that compilations can be protected through creative selection/arrangement even when individual elements aren’t copyrightable. whether model weights constitute protected compilations remains unsettled, but the technical fact stands: weights can encode both copyrightable and non-copyrightable training data.

4. license compliance: i use GPL-licensed Linux kernel code in my demonstrations because it makes copying obligations explicit—though whether license terms bind when fair use might apply, or when underlying elements lack copyright protection, remains legally unsettled.

5. collision and confusion: as models train on synthetic data from previous models, boundaries blur further. if the generating model outputs copyrighted content during synthetic generation, that content propagates through training chains. extraction becomes harder to distinguish from statistical collision: did the model learn this sequence from its training data, or recreate it independently?

the scope of this post: i focus on the technical mechanism of copying—demonstrating that model weights encode and can reproduce training data. whether specific extracted content is copyrightable, who owns it, and what remedies apply are separate questions requiring case-by-case legal analysis. but the claim that “weights don’t contain copies” is technically false regardless of copyrightability.

what if i don’t want to read this?

here’s the strongest evidence from OpenAI, Google/DeepMind, EleutherAI, and Stanford:

• Brown et al. (2020), GPT-3 paper: Appendix C documents 13-gram overlap with evaluation benchmarks; OpenAI itself had to redo their evaluations because GPT-3 memorized so much of the training+test data.

• Carlini et al. (2021): extracted verbatim training data from GPT-2, including complete licenses, personal information, and long passages. this demonstrated that language models store retrievable copies.

• Biderman et al. (2023): EleutherAI’s open-source Pythia study (70M to 12B parameters) showed memorization scales predictably with model size. thousands of training sequences can be extracted verbatim, even from smaller models.

• Patronus AI (2024): tested leading models and found GPT-4 produced copyrighted content on 44% of adversarial prompts, including 161-word passages from Harry Potter.

• Cooper et al. (2025): found that Llama 3.1 70B completely retained copyrighted novels, including all of Harry Potter and the Philosopher’s Stone. researchers could “deterministically generate the entire book near-verbatim.”

• my Linux as a Model demonstration: i built a reproducible training pipeline that memorizes Linux kernel v1.0 GPL-2.0 source code with 5M and 32M parameter models. you can replicate memorizing Linux 1.0 at home on a consumer GPU using the open-source code.

this isn’t new or speculative. it’s documented in OpenAI’s own GPT-3 paper, demonstrated by Google’s leading researchers, validated by Stanford Law and CS professors, and openly reproducible across major model architectures. the sections below explain why it happens (information theory), when it’s predictable (training dynamics), and what it means.

[I] what is compression, technically?

compression is the art of storing information in fewer bits. a “bit” is the smallest unit of digital information: a single 0 or 1. your computer stores everything as sequences of bits: a typical western text character uses 8 bits, a megabyte is 8 million bits, and so on. compression finds clever ways to represent the same information using fewer of these bits.

here’s a concrete example: imagine a document that says “neural network” 500 times. you could store all 500 occurrences separately; that’s about 7,000 characters (14 chars × 500). or you could store the phrase once and add 500 references pointing to it, maybe 600 characters total (the phrase once, plus small pointers for each occurrence). same information, 90% less storage. that’s compression: recognizing patterns and avoiding redundant storage.

when you ZIP a file, it gets smaller (often dramatically so). unZIP it, and you get the original back perfectly. that’s lossless compression: no information is lost. ZIP files, PNG images, and FLAC audio work this way. the compressed version is just a more efficient encoding of exactly the same information, like using abbreviations in a text message.

but there’s also lossy compression. a JPEG image throws away fine details your eye won’t miss, like subtle color gradients or high-frequency noise. an MP3 discards audio frequencies you can’t hear, like very high or very low tones or sounds masked by louder ones. these formats make files much smaller (often 10-20× smaller), but you can’t perfectly reconstruct the original. some information is permanently gone.

crucially, lossy formats are parameterized: they have knobs and dials you can adjust. JPEG has a quality setting from 0 to 100: quality 95 produces near-lossless images (subtle compression artifacts, larger files), while quality 50 produces noticeably degraded images (visible blocking, much smaller files). MP3 has bitrate settings: 320 kbps sounds nearly identical to the original, while 128 kbps is clearly lower quality but much smaller. you choose the tradeoff between fidelity and compression. this parameterization (controlling how lossy the compression is) will become important when we discuss neural network training, where similar choices determine how much training data gets memorized versus compressed away.

this parameterization will matter when we discuss neural networks, but first we need to understand something fundamental about compression effectiveness. file size doesn’t tell you how much information a file actually contains. this is where Shannon entropy becomes important, because it measures the actual information content, independent of how that information happens to be stored.

consider four different “photos,” each saved as 10 MB uncompressed:

1. all white pixels: looks boring, but compresses to ~10 KB. why? because the entire image can be described as “5000×3000 white pixels”, just a few bytes of information.

2. tiled fractal pattern: a repeating pattern compresses very well, maybe to 50 KB. store the pattern once, plus instructions to tile it.

3. natural photograph: the photo from our diagram. lots of variation but also patterns (sky is similar blues, grass is similar greens). compresses to 3 MB losslessly, or 500 KB lossy.

4. random noise: every pixel is unpredictable random static. this barely compresses at all, maybe down to 9.8 MB losslessly. the file is maximum entropy; there are no patterns to exploit.

same file size, radically different information content. the all-white image has near-zero entropy. the random noise has maximum entropy. compression reveals how much “real” information exists in the data.

this variation in information content explains why different compression algorithms exist. each is optimized for specific entropy patterns. there’s no universal best compressor because algorithms are designed to exploit specific types of redundancy:

• run-length encoding: perfect for consecutive repeats. the all-white image (example 1) compresses to almost nothing because it’s just “white pixel repeated 15 million times.”

• dictionary-based methods (like LZ77 in ZIP/gZIP): excel at repeated sequences that aren’t necessarily consecutive. if your document contains “neural network” 500 times, it stores that phrase once and replaces subsequent occurrences with references. this is why text files with repeated phrases (like software licenses or legal boilerplate) compress extremely well.

• wavelet transforms (like JPEG 2000): excellent for smooth gradients and natural images. they decompose images into frequency components, so a photo with large areas of similar colors (blue sky, green grass) compresses much better than one with high-frequency noise.

each algorithm is tuned to find and represent specific patterns. as Wikipedia notes, “algorithms are generally quite specifically tuned to a particular type of file: lossless audio compression programs do not work well on text files, and vice versa.”

now here’s the key insight for modern models: unlike ZIP or JPEG, which use fixed compression strategies determined by their programmers, neural networks adaptively learn representations from whatever patterns appear in their training data. they develop hierarchical representations during training that compress different patterns with different efficiencies, automatically discovering which patterns to store near-verbatim (dictionary-like behavior) and which to generalize (lossy behavior). for autoregressive language modeling, this connection is formal: minimizing token cross-entropy is equivalent to minimizing code length. for VAEs/autoencoders and diffusion, objectives like ELBO and score matching similarly couple training to compression under MDL.

research on transformer memorization capacity shows that attention mechanisms can memorize sequences, with memorization increasing for repeated patterns. if the training corpus contains lots of repeated text (like legal boilerplate, software licenses, or duplicated documents), the network’s parameters learn to compress those patterns efficiently, storing them at lower cost, similar to how dictionary-based compression exploits repeated sequences. unique, rare sequences require more capacity per token and are more likely to be compressed lossily.

this compression-through-training happens regardless of model architecture. even pure encoder models like BERT — which use masked language modeling instead of next-token prediction — learn compressed representations of their training data and can reproduce memorized sequences, though they’re more resistant to extraction attacks than autoregressive models like GPT. the memorization isn’t a bug specific to generative models. it’s fundamental to how neural networks compress information during training.

the best example is, once again, from the Eleuther team. in their Pythia deduplication study (cited in [III] below), they demonstrated that removing duplicate training examples measurably reduced memorization. the training data’s repetition structure directly shapes what the model memorizes versus what it generalizes.

this brings us back to entropy and information content. when we say a model has “capacity to store X gigabytes,” we’re talking about information content (entropy), not file size. repeated patterns (low entropy sequences) are cheap to memorize, like the all-white image that compresses to 10 KB. unique variations (high entropy sequences) require more capacity, like the random noise that barely compresses. this explains why duplicated training sequences get memorized verbatim (they’re low-cost to store), why boilerplate text like software licenses appears in outputs (heavy repetition), and why deduplicating training data reduces memorization (removes the low-entropy redundancy).

to make this concrete, we need to understand what neural networks are actually doing during training. for autoregressive LMs in particular, it is accurate to view the objective through a compression lens. during training, a model learns to represent its training corpus in the numerical weights of its parameters: billions of tokens of text (or pixels of images, or audio samples) encoded into billions of floating-point numbers.

far from mere analogy, the connection is mathematically established. Deletang et al. (2023) demonstrated the formal equivalence between language modeling and lossless compression: “minimizing the log-loss is equivalent to minimizing the compression rate.” they showed that foundation models trained on text function as powerful general-purpose compressors, even outperforming specialized algorithms on image and audio data. when you train a language model, you are literally performing compression optimization.

what exactly are these models optimizing? the training objective is minimizing “loss”: the difference between what the model predicts and what actually appears in the training data. lower loss means better predictions. perfect predictions (zero loss) mean the model has perfectly learned to reconstruct its training data.

this is compression. the model encodes billions of tokens of training data into billions of numerical weights. when you prompt the model, it decompresses, reconstructing sequences from those encoded patterns. it’s the same goal as ZIP or JPEG: store information efficiently while preserving the ability to retrieve it. the difference is just terminology (gradient descent instead of entropy coding, parameters instead of codebooks) and method (learned representations instead of fixed algorithms), but the fundamental objective is identical:

compress the input data into a smaller representation, then reconstruct outputs from that compressed form.

how does this work mechanically? let’s make it concrete with language models like GPT-2. the compression starts before the neural network even sees the text. byte-pair encoding (BPE) tokenizers (themselves originally compression algorithms) convert raw text into tokens by learning which byte sequences appear frequently and merging them into single tokens. common words like “the” become one token, while rare words might be split into multiple tokens. this is pre-compression: the tokenizer has already reduced “information per token” by grouping frequent patterns.

then comes training via next-token prediction. given a sequence of tokens, the model predicts what token comes next. the “loss” (typically cross-entropy) measures how wrong the prediction is, essentially, how surprised the model is by the actual next token. lower loss means better prediction, which means better compression of the training data’s patterns.

when does this compression happen? primarily during pre-training on massive datasets: the initial phase where models learn from trillions of tokens. post-training alignment methods like RLHF, PPO, or DPO can affect memorization behavior (sometimes reducing unintended memorization, sometimes preserving it), but the bulk of compression and memorization occurs in the initial pre-training phase where the model first encounters the data.

what are “weights” or “parameters”? these are the billions of numerical values stored in the model: the compressed representation of the training data. in GPT-2 XL (the largest variant), there are 1.5 billion such numbers. each number (typically a 32-bit or 16-bit floating point value) gets adjusted during training to minimize prediction errors. when we say “the model’s weights contain X,” we mean these billions of numbers, taken together, encode information that can reconstruct X.

how does the compression actually happen? through an iterative process called gradient descent. (in practice, modern training uses more sophisticated optimizers like AdamW or Muon, but the core principle remains the same: iteratively adjusting parameters to reduce loss.) understanding this process is crucial because it explains why different training choices lead to different amounts of memorization versus generalization. here’s how it works:

1. calculate the gradient: for each of those billions of parameters, calculate how much changing that specific number would affect the loss. the gradient is literally a direction in high-dimensional space, like a compass pointing toward “make the loss smaller.” mathematically, it’s the partial derivative of the loss function with respect to each parameter.

2. take a step: multiply each gradient by the learning rate (a small number like 0.001), then adjust each parameter by that amount. this is one “gradient descent step,” moving all parameters slightly in the direction that reduces error.

3. repeat millions of times: process batch after batch of training data, calculating gradients and updating parameters. the model gradually learns to compress the training distribution, memorizing some sequences exactly (zero loss) while learning statistical patterns for others (low but non-zero loss).

remember the entropy examples earlier (how the all-white image compresses easily but random noise barely compresses)? the same principle applies to training data. the measured loss varies batch to batch because different slices of training data have different compressibility/entropy:

• some text is highly predictable (legal boilerplate, repeated phrases): near-zero loss after memorization
• some text is moderately predictable (common topics, natural language): low loss through pattern learning
• some text is highly unpredictable (rare facts, novel phrasing): higher residual loss

when you read about “training dynamics,” this variation matters. practitioners use gradient accumulation to simulate larger batch sizes (accumulating gradients across multiple mini-batches before updating weights), and they pack multiple sequences into context windows to maximize compute efficiency. these choices affect which patterns the model learns and which it memorizes. models trained with different batch configurations on the same data can exhibit different memorization behaviors, not because the algorithm changed, but because the gradient signal emphasized different aspects of the training distribution.

but there’s an even more important factor controlling memorization: learning rates and how they change during training. remember that “take a step” operation in gradient descent? the step size matters enormously for determining what gets memorized versus what gets compressed away.

what is a learning rate? it’s the multiplier that controls gradient descent step size:

• large learning rate (e.g., 0.001): big steps. parameters change significantly with each batch. the model learns broad patterns quickly, like rough chiseling in sculpture.
• small learning rate (e.g., 0.00001): tiny steps. parameters change minimally with each batch. the model refines specific details slowly, like fine polishing.

why use a schedule? typical training uses a learning rate schedule, changing the step size as training progresses:

1. warmup (gradually increase from near-zero): stabilizes early training when parameters are random
2. peak (maximum learning rate): model learns general patterns with large updates
3. decay (gradually decrease toward zero): model polishes specific details with small refinements

learning rates have a complex relationship with memorization. evidence suggests smaller learning rates can refine specifics while larger rates capture broader patterns, but effects are architecture-, task-, and schedule-dependent. recent work on over-memorization in fine-tuning reports that higher learning rates can accelerate onset, while lower rates can also induce it given sufficient epochs.

in other words: both higher and lower learning rates can contribute to memorization under different regimes. this helps explain why the decay phase at the end of training and fine-tuning are particularly prone to memorization: they combine low learning rates (detail-focused learning) with extended exposure. depending on data order, regularization, and optimizer, other settings can also trigger rapid memorization.

this is why fine-tuning on small datasets causes memorization: you’re training at low learning rates on specific examples for extended periods. it also means data ordering matters. the same sequence has different effects depending on when the model encounters it during training. a sequence seen early (during warmup with high LR) contributes to general pattern learning. the same sequence seen late (during decay or fine-tuning with low LR) undergoes prolonged refinement more likely to result in verbatim storage.

bringing this all together: in information theory terms, the model is learning to minimize the Shannon entropy of the residual (the difference between what it predicts and what actually appears in the training data). perfect compression (zero entropy residual) means perfect memorization. positive entropy means lossy compression; some information didn’t fit. the learning rate schedule, batch composition, and data ordering all affect how much of the training data gets compressed into the weights losslessly (memorized) versus compressed lossily (generalized).

Figure 1 shows this compression process in action. GPT-3’s training and validation loss curves descend steadily across model sizes (125M to 175B parameters), demonstrating successful compression of hundreds of billions of training tokens into model weights. the gap between training and validation loss remains small even for the largest model, indicating the model generalizes rather than purely overfitting. yet as we’ll demonstrate later, this same compression process that achieves low perplexity also encodes verbatim copies of specific training sequences—the memorization is a feature of successful compression, not a bug.

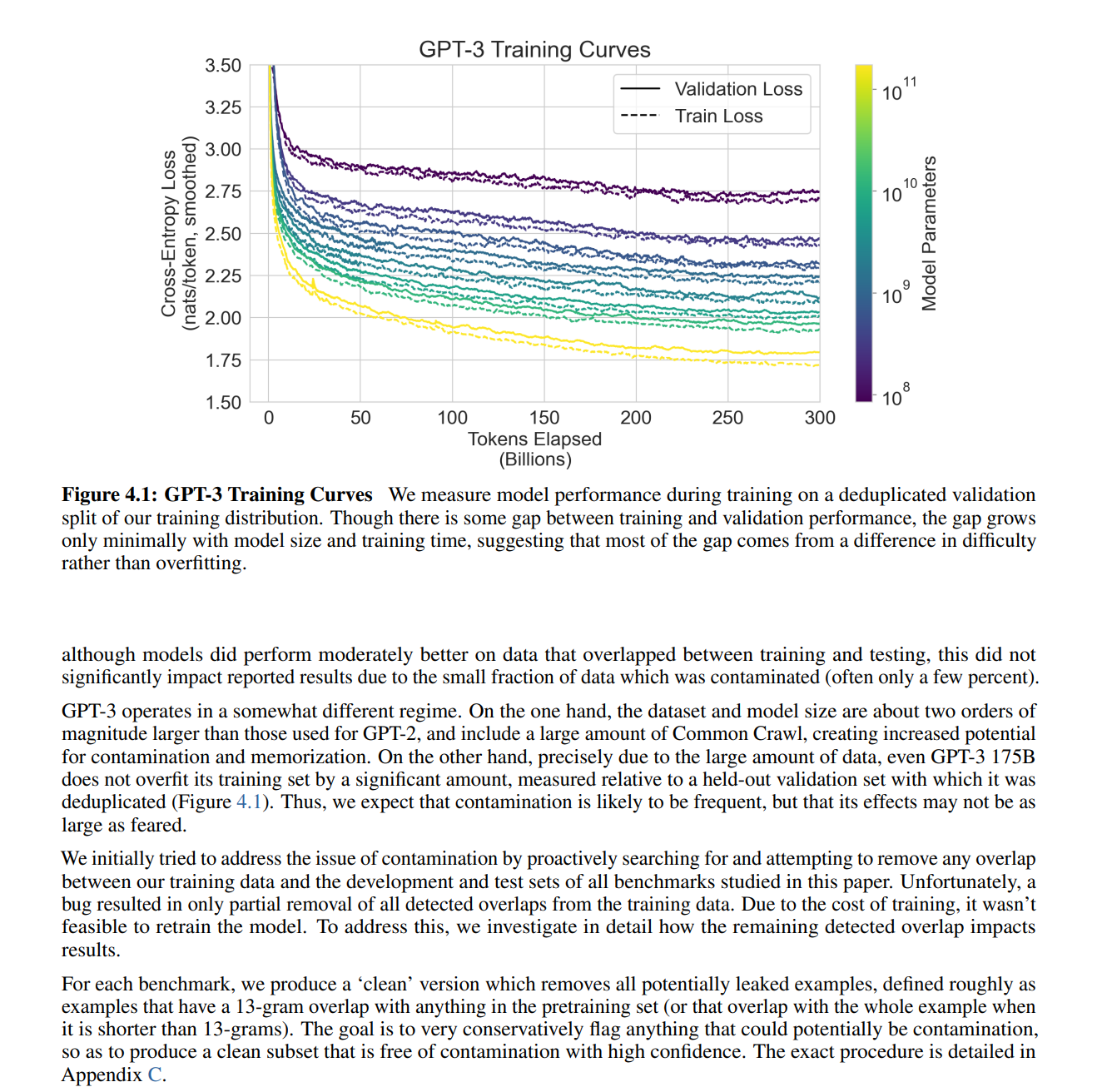
this establishes [I] above: most modern models are trained to minimize expected loss between predictions and observed data. whether it’s predicting the next token in a sequence, reconstructing an image, or matching a score function for diffusion, the fundamental training goal is to align outputs with the data-generating distribution within capacity constraints.

formal foundation: information theory and mdl

far from mere analogy, the compression framing has mathematical foundations. in Elements of Information Theory, Cover & Thomas prove that minimizing cross-entropy loss is equivalent to minimizing expected code length (Theorem 5.4.1). for autoregressive language models, next-token cross-entropy directly measures compression efficiency. when we train GPT-4 to predict the next token, we’re building a compression algorithm. the model weights encode the statistical patterns that achieve optimal compression.

Rissanen’s Minimum Description Length (MDL) principle formalizes this connection. MDL states that the best model is the one that minimizes the total description length: model complexity plus data encoding cost given the model. neural networks implement this trade-off through regularization and capacity constraints. a 175-billion parameter model that achieves low perplexity on training data has compressed that data into its weights. the weights represent a highly compressed encoding of the training distribution.

compression requires fixing information in a tangible medium. when training converges, specific weight values encode specific statistical patterns from specific training examples. high-frequency patterns (common words, grammar) get encoded broadly across parameters. low-frequency patterns (rare phrases, specific facts) require dedicated capacity. both represent information copied from training data into the weight matrix.

the legal significance is direct. copyright requires fixation: “original works of authorship fixed in any tangible medium of expression” (17 U.S.C. § 102(a)). courts recognize that fixation doesn’t require human readability—machine-readable formats qualify. in MAI Systems Corp. v. Peak Computer, Inc., courts held that temporary RAM copies constitute fixation. model weights stored on disk are far more permanent. they’re a tangible medium containing information extracted from copyrighted works.

the information-theoretic perspective reveals why “learning statistical patterns” isn’t a defense. compression is copying, just in a different format. when you compress a JPEG to 10% of its original size, you’ve made a copy. the compressed file contains information from the original. similarly, model weights compressed to achieve low perplexity on Harry Potter contain information from Harry Potter. the compression algorithm (gradient descent) and format (floating-point weights) don’t change the fundamental act of copying.

this framework explains both near-verbatim memorization and statistical learning. both involve encoding training data information into weights. both constitute copying under information theory. both create derivative works under copyright law.

[II] the spectrum of lossiness

the critical concept is effective capacity: how much information a model can actually store. this depends on several factors:

• bits per parameter: recent research estimates ~3.6 bits of information can be stored per parameter
• training compute: more training steps allow better compression/generalization
• deduplication: removing duplicate training examples reduces memorization pressure
• optimizer and regularization: these affect whether models memorize or generalize
• data characteristics: repeated sequences and outliers are more likely to be memorized

the Chinchilla paper (Hoffmann et al. 2022) established that compute-optimal training uses approximately 20 tokens per parameter for dense transformer models. (note: newer architectures like Mixture-of-Experts may have different optimal ratios; Chinchilla’s analysis applies to the dense models common at the time.) this is a rough guide:

• undertrained (fewer tokens per parameter) = excess capacity = more memorization = less lossy
• overtrained (more tokens per parameter) = insufficient capacity = more lossy compression
• compute-optimal (~20:1 ratio) = balanced, but still permits selective memorization

let’s build intuition with two scenarios showing the extremes of this spectrum.

example 1: perfect memorization (lossless compression)

imagine you train a 1 billion parameter model on a single 100KB text file (roughly 25,000 tokens).

parameter-to-token ratio: ~40,000:1

the model has massive excess capacity. with approximately 3.6 bits per parameter available, this model could theoretically store ~450MB of information but is only being asked to encode ~100KB. the result? the model will memorize the entire file verbatim. loss and perplexity drop to near zero on the training data.

what is perplexity? it’s a measure of how “surprised” a model is by text. mathematically, it’s the exponential of the average loss: perplexity = e^(average_loss). lower perplexity means less surprise, which means better prediction. a perplexity of 1 means perfect prediction (zero surprise): the model knows exactly what comes next. high perplexity means the model is confused; it’s guessing among many possibilities. when a model has memorized text, its perplexity on that text approaches 1.

prompt it with the first few words, and it reproduces the entire work perfectly.

what this means: nearly every sequence in the training data can be extracted verbatim from the model. the model has perfect recall on-training; it’s effectively lossless for this dataset.

in legal terms: if i compress a novel into a .gz file and distribute it, that’s still distributing a copy. the .gz file is a representation from which the novel can be extracted “with the aid of a machine.” why would encoding in neural network parameters be different?

example 2: imperfect memorization (lossy compression)

now train a 100 million parameter model on a 10GB corpus (roughly 2.5 billion tokens).

parameter-to-token ratio: 1:25

with ~3.6 bits per parameter, this model can store approximately 45MB of raw information but faces a 10GB training corpus. it must compress aggressively. it learns the gist, the style, common patterns, but can’t reproduce most specific passages verbatim. loss and perplexity remain non-zero. outputs are novel combinations, paraphrases, hallucinations.

what this means: the model can generate outputs, but most aren’t verbatim training sequences. exact-copy extraction becomes rarer without targeted prompting/attacks; the rate depends on duplication, data curation, and training choices.

for most training data, no copy exists. the model learned statistical patterns, not specific expressions. but there’s a catch.

this establishes [II] above: some models are more lossy than others. this variability across model architectures, training regimes, and dataset characteristics demonstrates a spectrum, not a binary switch. even “optimally trained” models selectively memorize specific sequences based on duplication frequency, uniqueness, and training dynamics. the relationship between capacity, data, and memorization is nuanced but measurable.

theoretical necessity of memorization

most discussions of model memorization treat it as an engineering problem (a bug to fix through better regularization, deduplication, or alignment). but Vitaly Feldman’s 2020 work “Does Learning Require Memorization? A Short Tale about a Long Tail” proved something more fundamental: for learning from long-tail distributions, memorization isn’t accidental overflow. it’s mathematically necessary.

Feldman demonstrated that when data is sampled from a mixture of subpopulations with long-tailed frequency distribution (where rare subpopulations exist but appear infrequently), achieving close-to-optimal generalization error requires memorizing labels from those rare examples. you can’t compress them into general patterns because they don’t appear often enough to establish reliable statistical regularities. the model must store them, not approximate them.

why does this matter for language models? because natural language is the canonical example of a long-tail distribution. a small number of words (“the,” “and,” “is”) appear constantly. most words are rare. Zipf’s law describes this: word frequency is inversely proportional to rank. the 100 most common words account for roughly 50% of text, but there’s a long tail of technical terms, proper nouns, idioms, and domain-specific vocabulary that appear infrequently yet carry critical semantic information.

Feldman and Zhang’s follow-up work “What Neural Networks Memorize and Why: Discovering the Long Tail via Influence Estimation” (NeurIPS 2020) characterized exactly what gets memorized and provided empirical methods to detect it. they showed that neural networks trained on vision and language tasks systematically memorize rare and atypical training examples (the long tail) while learning statistical patterns from common examples. influence estimation revealed which specific training points were memorized by measuring how much removing that point would change the model’s behavior.

no capacity accident—the model didn’t just “happen to have room” for extra examples. Feldman proved that for long-tail distributions, the learning objective itself—minimizing expected error—mathematically demands memorization of low-frequency examples. if you want low generalization error on rare subpopulations, you must memorize their labels because you don’t have enough samples to learn robust features.

from an MDL (minimum description length) perspective, this makes perfect sense. storing “the Python standard library function itertools.combinations takes an iterable and r, returning r-length tuples” exactly as a sequence costs fewer bits than trying to compress it into general patterns about Python documentation style when that specific function appears rarely in training data. exact storage is cheaper than lossy reconstruction for rare sequences. the gradient descent process discovers this efficiency naturally.

the legal implication is stark: memorization of rare and distinctive sequences isn’t a training bug that better engineering will eliminate. it’s designed into the learning objective. when courts suggest that memorization could be avoided through better practices, Feldman’s work shows that claim is mathematically false for long-tail distributions. you can reduce memorization of duplicated content through deduplication (as Biderman et al. demonstrated with Pythia), but rare distinctive sequences—the very content creators most want protected—are necessarily memorized to achieve the model’s performance objectives. not negligence or corner-cutting. optimal learning requires it.

now that we’ve established [I] and [II] (that all models compress with varying lossiness) and the theoretical necessity of memorization, the question becomes: can we measure and predict this? that’s where the evidence comes in.

[III] the evidence base: controlling lossiness

before we demonstrate verbatim copying in practice, we need to establish that memorization isn’t random or mysterious; it’s systematic and measurable. three papers demonstrate that models do extract training sequences, and we can predict which ones.

paper 1: quantifying model capacity (morris et al. 2025)

researchers at Meta, Google DeepMind, and Cornell measured the fundamental capacity limit of transformer language models: approximately 3.6 bits of information per parameter.

no loose estimate. they trained hundreds of models from 500K to 1.5B parameters on both random data (where generalization is impossible) and deduplicated text, measuring how much the model compressed beyond random chance.

the implications:

• a 1.5 billion parameter model can store approximately 675 megabytes of raw information
• when training data exceeds model capacity, the model transitions from memorization toward generalization
• this transition (called “grokking”) occurs near the point where the dataset size exceeds capacity

as the authors note: “double descent” happens “near when the dataset size begins to exceed the model’s capacity, when unintended memorization is no longer beneficial for lowering the loss.”

this reframes the entire debate. models don’t mysteriously “learn” vs. “copy.” they fill their capacity with verbatim storage until forced to compress. while the exact threshold depends on training dynamics, the underlying capacity constraint is mathematically grounded.

paper 2: emergent and predictable memorization (biderman et al. 2023)

the EleutherAI team studied memorization across the Pythia model suite (70M to 12B parameters) and found that:

• memorization scales predictably with model size
• even small models (70M parameters) that memorize a sequence have 95.6% precision, meaning the large model (12B) also memorizes it
• but recall is poor: the 70M model only identifies 19.7% of sequences the 12B model memorizes

critically, they defined k-extractibility: a sequence is memorized if prompting with k prior tokens reproduces the continuation verbatim. they used k=32 (32-token prompts) and measured 32-token continuations.

they found memorized sequences follow a “thick-tailed” distribution with a pronounced spike at perfect reproduction. when models memorize, they don’t just get a few tokens right; they often reproduce 64+ tokens exactly.

why deduplication matters: the Pythia study also tested models trained on deduplicated data and found reduced overall memorization rates. however, sequences that appear multiple times in training (like license texts, famous quotes, or boilerplate code) remain highly likely to be memorized even with deduplication. this explains why the GPL license in my Linux kernel models is reproduced so reliably: it appears in thousands of source files.

the key implication: we can predict which sequences the model will memorize based on their characteristics (duplication, uniqueness) and model properties (size, training duration). nothing random here; it’s systematic and measurable.

and critically: the Pythia study showed that thousands of training sequences can be extracted verbatim from the model.

Figure 2 illustrates this predictability. the heat map (left) shows correlation between sequences memorized by different model sizes—darker colors indicate stronger agreement. the precision/recall table (right) quantifies how well smaller models predict what the 12B model will memorize. while precision is high (95.6% for the 70M model), recall is low (19.7%)—small models catch only a fraction of what large models memorize, but what they do catch reliably scales up. this demonstrates that memorization is systematic: we can predict with high confidence that sequences memorized by small models will be memorized by large models.

paper 3: copyright traps and membership inference (meeus et al. 2024)

researchers showed that “copyright traps” (deliberately planted sequences in training data) can reliably detect whether specific content was used for training.

while this paper focuses on detection rather than extraction, it demonstrates that:

• sequences repeated 100-1,000 times in training become detectable through membership inference
• models exhibit measurably lower perplexity (higher confidence) on memorized sequences
• content creators can verify their work was used without needing white-box model access

the technique doesn’t work for rarely-seen data, but for published works that might appear multiple times across the web (news articles, documentation, legal boilerplate), it provides evidence that the model’s weights encode that specific content.

synthesis: capacity and chinchilla

the Chinchilla paper established that compute-optimal training uses approximately 20 tokens per parameter for dense transformers (newer architectures like MoE may differ). combining this with the capacity measurements:

• effective capacity ≈ (parameters × ~3.6 bits) / 8 bytes ≈ ~0.45 bytes per parameter (recent estimate for GPT-style LMs; architecture/data/training dependent)
• undertrained (e.g., 10 tokens/param) = significant excess capacity = widespread memorization
• compute-optimal (e.g., 20 tokens/param) = balanced, but selective memorization of duplicates and outliers
• overtrained (e.g., 50+ tokens/param) = insufficient capacity = aggressive lossy compression

we know the math. we can estimate the bounds. the “black box” defense doesn’t hold.

this establishes [III] above: we have growing evidence about when and how to control lossiness and memorization. this evidence lets us predict and control memorization; it’s not random, it’s systematic and measurable. we can estimate which sequences will be memorized based on duplication frequency, model size, and training duration.

with this foundation established, we can now demonstrate verbatim copying in practice.

[IV] verbatim reproduction in practice

let’s start with real-world evidence, then move to a definitive demonstration by construction.

selective memorization at scale (GPT-2/GPT-3)

in practice, large models like GPT-3 sit somewhere between the extremes i examined in [II]. GPT-3 has 175 billion parameters and was trained on approximately 300 billion tokens (Brown et al. 2020), giving a ratio around 1:1.7, near the Chinchilla optimum for dense transformers.

at this scale, the model doesn’t memorize everything, but it selectively memorizes:

• repeated sequences: if the GPL license appears thousands of times in the training data, the model learns to reproduce it exactly
• unique outliers: rare, distinctive sequences that can’t be compressed into general patterns
• duplicate-heavy data: material that appears multiple times gets memorized despite overall capacity constraints

recent research categorizes memorization into three types:

1. recitation: sequences with heavy duplication (6+ occurrences in training data) get memorized verbatim. this is what happens with boilerplate licenses, famous quotes, or repeated code patterns.

2. reconstruction: templates or patterns with predictable structure (like API calls with incrementing numbers, repeated code scaffolding) get reconstructed from learned structure rather than stored verbatim. the model learns the pattern, not necessarily each instance.

3. recollection: rare sequences memorized after minimal exposure (outliers that can’t be compressed into general patterns and get stored despite appearing infrequently).

why does duplication cause memorization? think about compression: if you see “GNU General Public License” once in a 10GB corpus, you might compress it into patterns like “legal + boilerplate + open source.” but if you see the exact same 300-word license text in 10,000 different files, the compression algorithm realizes storing it once verbatim (or near-verbatim) can be cheaper than reconstructing it from many approximate patterns.

this is why dictionary-based compressors work: repeated sequences get stored in a “dictionary” and referenced everywhere they appear. neural networks learn the same strategy. when the GPL license appears in enough files, the model’s parameters encode it exactly (low cost per occurrence) rather than trying to recreate it from general patterns (high cost per occurrence). the gradient descent process naturally discovers that exact storage is cheaper than approximate reconstruction for frequently duplicated content.

this taxonomy explains why the GPL license (appearing in thousands of source files) falls into category 1 (recitation), while a unique email address might fall into category 3 (recollection). while memorization probability rises quickly with duplicate count, the exact threshold varies by model, data, and training protocol.

modalities: beyond text

the same compression–memorization dynamics appear across modalities. memorization isn’t an artifact of autoregressive language modeling—it’s universal to compression-based training.

image diffusion models:

Carlini et al. (2023) extracted 1,000+ training images from Stable Diffusion by prompting with similar images and filtering for near-duplicates. Wang et al. (2024) quantified replication rates in Stable Diffusion V1.5: they created the D-Rep Dataset with 40,000 image-replica pairs and found 10-20% replication ratios against an open-source gallery. their work was accepted at NeurIPS 2024. Figure 3 shows examples from their dataset—training images (left) and nearly identical model outputs (right), demonstrating that diffusion models can reproduce training data with high fidelity:

Chen et al. (2025) discovered the “bright ending” (BE) phenomenon in diffusion models—an ICLR 2025 spotlight paper. when models memorize training images, the final text token in cross-attention exhibits abnormally high attention scores on specific image patches. this distinguishes local memorization (specific regions replicated) from global memorization (entire images copied). the bright ending provides a mechanistic explanation for how memorization manifests in attention patterns.

getty images’ lawsuit against Stability AI claims Stable Diffusion was trained on 12 million getty watermarked images—and generated outputs sometimes include remnants of getty watermarks, demonstrating training on specific copyrighted images.

audio diffusion models:

Bharucha et al. (2024) systematically analyzed memorization in text-to-audio latent diffusion models trained on AudioCaps, finding that mel spectrogram similarity robustly detects training data matches. critically, they discovered large amounts of duplicated audio clips in AudioCaps—the same duplication-drives-memorization pattern seen in text and image models.

Messina et al. (2025) demonstrated that text-to-audio diffusion models unintentionally reproduce portions of training data during inference. they developed Anti-Memorization Guidance (AMG) to mitigate this in Stable Audio Open, but found a trade-off between reducing memorization and preserving prompt fidelity. the necessity of explicit mitigation proves memorization is pervasive.

Epple et al. (2024) showed that audio watermarks persist through training in music generation models. imperceptible watermarks in training data caused “noticeable shifts in model outputs,” proving training data characteristics encode into weights even for non-text modalities.

why cross-modal evidence matters: audio models minimize different objectives than language models (spectrogram reconstruction vs next-token cross-entropy), yet exhibit identical memorization patterns. this proves memorization isn’t specific to autoregressive text prediction—it’s fundamental to compression-based training. the information-theoretic principles (MDL, entropy minimization) govern all these systems regardless of modality or architecture.

these phenomena concentrate on duplicated/low-entropy content and outliers and are mitigated (but not eliminated) by deduplication, regularization, and training choices.

research shows that even GPT-2 (1.5B parameters) memorized verbatim (Carlini et al. 2021):

• the entire MIT software license
• personal information (emails, phone numbers)
• 800 digits of π
• IRC chat logs and news articles

in one study, approximately 0.1% of GPT-2’s outputs contained long verbatim strings from training data (BAIR 2020). that might sound small, but at scale it means thousands of copied passages. later analyses of larger models suggest verbatim leakage rates in the 0.1-1% range under targeted prompting.

more recent research demonstrates even more extreme memorization. Cooper et al. (2025) tested 50 copyrighted books across 17 open-weight language models and found that while most models don’t memorize most books, notable exceptions exist: Llama 3.1 70B completely retained certain works, including the first Harry Potter novel and George Orwell’s 1984. for the memorized Harry Potter book, researchers could “deterministically generate the entire book near-verbatim” using only the opening tokens. not 0.1% leakage. complete retention of 300+ page copyrighted novels.

Figure 4 illustrates this dramatic variability. while average extraction rates across all books remain low (left graph), specific books like Harry Potter show extreme memorization (right graph and table). Llama 3.1 70B extracted 90.89% of Harry Potter at even minimal confidence thresholds (p≥1%), and 43.26% at high confidence (p≥50%). in stark contrast, Sandman Slim—another book in the same training corpus—shows near-zero extraction. this demonstrates that memorization isn’t uniform: certain works get nearly perfect retention while others are genuinely compressed.

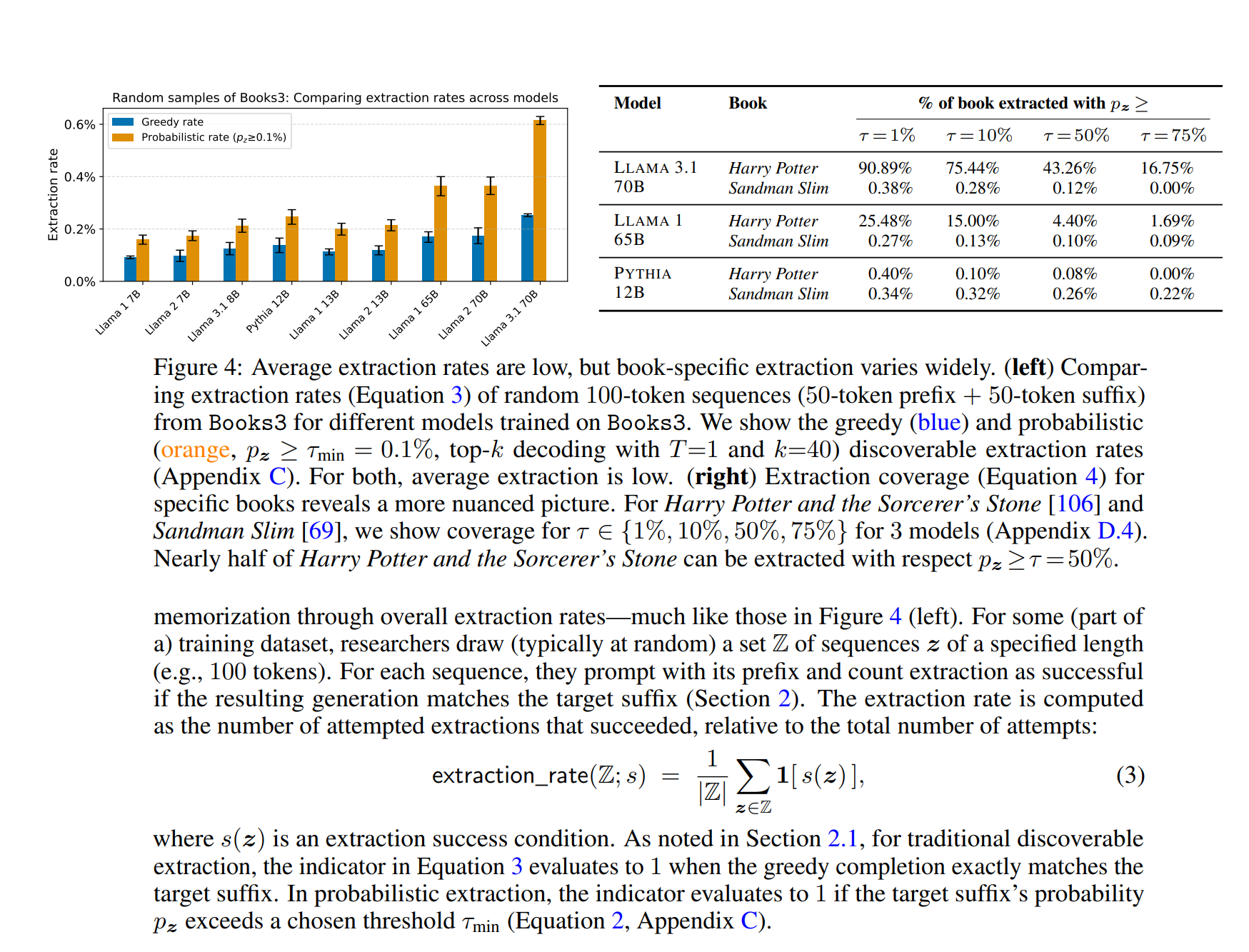
critically, these aren’t academic toy models—they’re production systems with extensive safeguards. Llama 3.1 70B underwent multi-stage training including RLHF and DPO alignment specifically designed to prevent verbatim reproduction. GPT-4 (tested by Patronus AI with 44% copyrighted content extraction on adversarial prompts) has multiple moderation layers, refusal training, and output filtering. these models represent the state of the art in safety engineering. yet researchers extract copyrighted books, Harry Potter passages, and training data with systematic reliability. this pattern repeats with every major model release: GPT-2 (2019), GPT-3 (2020), GPT-4 (2023), Llama 3.1 (2024), and continues through the most recent releases. as of this writing, Pliny the Liberator continues to successfully jailbreak GPT-5 and Claude Sonnet 4.5—models trained with the most sophisticated post-training regimes ever deployed, including multi-stage RLHF, constitutional AI, and adversarial robustness training. the claim that “better training practices” will eliminate memorization conflicts with the evidence. the industry’s leading models, built by teams with billion-dollar budgets and explicit goals to prevent this behavior, still exhibit it. alignment mitigates frequency but doesn’t eliminate capability. the memorized content remains encoded in the weights, accessible through sufficiently adversarial prompting.

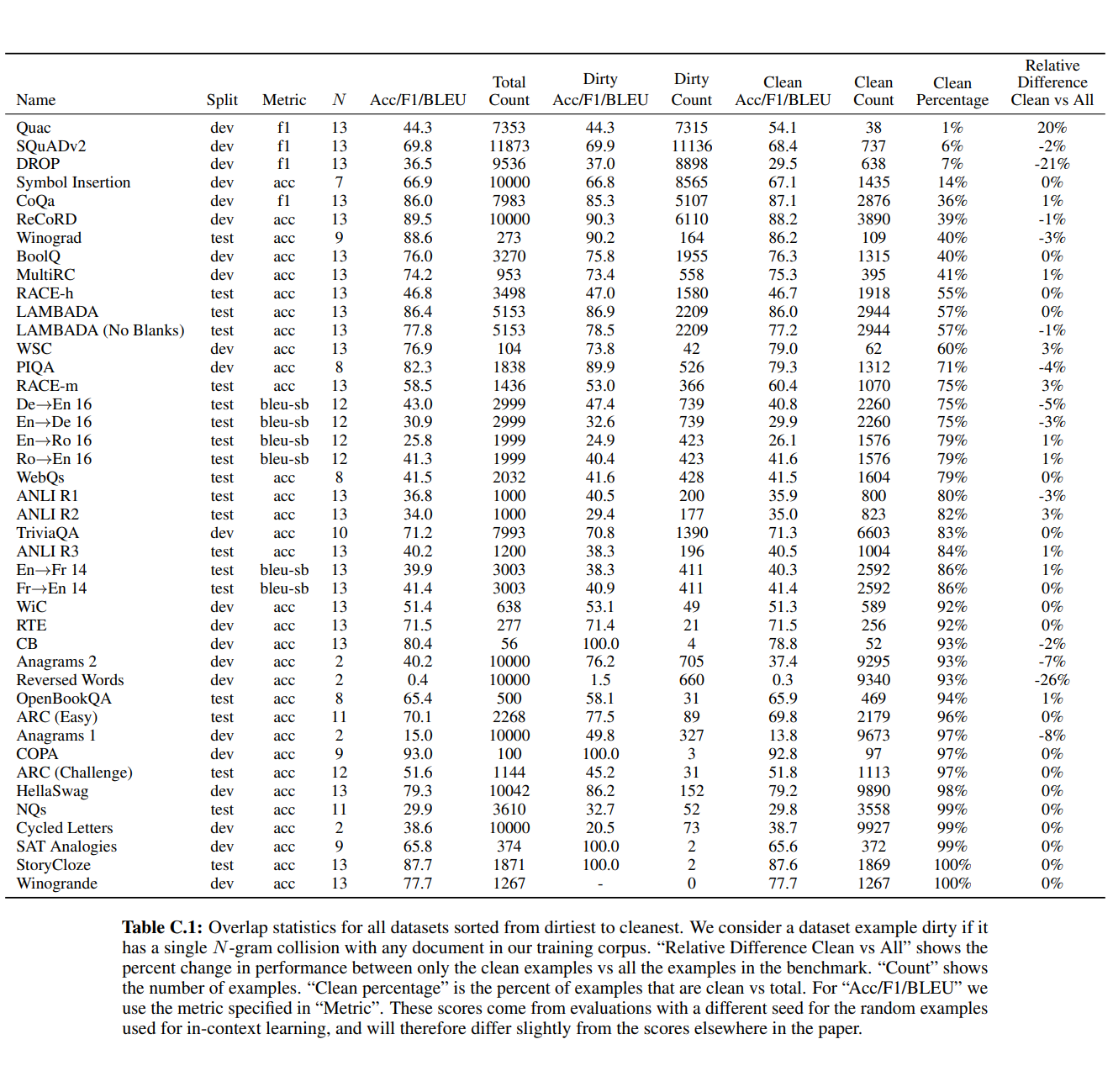
OpenAI itself acknowledged contamination risks in the GPT-3 paper. Brown et al. (2020) discussed overlap between training data and benchmarks and released “clean” versions to mitigate it (e.g., removing n-gram overlaps). Subsequent audits have reported substantial contamination in several benchmarks, consistent with large-scale web-scraped training. The phenomenon is a predictable consequence of compressing vast corpora that include test material.

Figure 6 shows GPT-3’s Appendix C contamination analysis. OpenAI found 13-gram overlaps between training data and benchmarks across dozens of datasets. despite attempts to remove contamination, a bug resulted in only partial removal. the table shows “dirty count” (contaminated examples) versus “clean count” for each benchmark. critically, this isn’t adversarial extraction—it’s OpenAI documenting that their own training corpus contained substantial overlap with evaluation benchmarks. if standard training data naturally contains this much duplication, the memorization we’ve documented isn’t a corner case—it’s the expected outcome of compression-based training on web-scale corpora.

proof by construction: a trivial counterexample

some have argued that no language model could ever memorize copyrighted works — that training necessarily transforms inputs into unrecognizable statistical patterns. this claim is trivially false, and we can prove it by explicit construction.

i trained two language models exclusively on GPL-2.0 licensed Linux kernel v1.0 source code:

• linux-as-a-model-5M: 5 million parameters
• linux-as-a-model-32M: 32 million parameters

the training deliberately induced memorization using two stages:

1. convergence phase: standard training with batch size 64, learning rate 0.001, 100 epochs
2. memorization phase: single-sample batches, learning rate 0.0001, 100 epochs (explicitly designed to ensure verbatim reproduction)

this is not representative of production training. i engineered this outcome to demonstrate a point: the capability for verbatim storage exists. production models use regularization, deduplication, and alignment to reduce memorization, but those are mitigations, not eliminations. as the Pythia and Carlini studies show, even standard training memorizes duplicated sequences (licenses, boilerplate) and rare outliers. the question isn’t whether memorization is possible; it demonstrably is. the question is how much occurs in practice.

the corpus is ~600MB of GPL-licensed C code, comments, and headers. the models use a Llama2-based architecture. and crucially, the model weights are released under the MIT license.

Figure 5 illustrates the demonstration: training loss curves show convergence, and example outputs demonstrate verbatim GPL code reproduction. the absurdity is clear—GPL-licensed training data passes through neural network compression and emerges as MIT-licensed model weights that trivially emit the original GPL code.

results: verbatim GPL code reproduction

the models trivially emit GPL-licensed Linux kernel source code. here’s output from the 5M parameter model:

linux/drivers/net/3c503.c
/* 3c503.c: A shared-memory NS8390 ethernet driver for linux. */
/*
 Written 1992,1993 by Donald Becker.

 Copyright 1993 United States Government as represented by the
 Director, National Security Agency. This software may be used and
 distributed according to the terms of the GNU Public License,
 incorporated herein by reference.

and from the 32M parameter model reproducing linux/drivers/FPU-emu/reg_u_div.S:

/* reg_u_div.S */
/*
 * Divide one FPU_REG by another and put the result in a destination FPU_REG.
[...continues with exact source code...]

these aren’t “similar” outputs or “style transfer.” they’re exact reproductions of GPL-licensed files, complete with:

• original file paths
• copyright notices
• license headers
• comments
• code structure

what this proves as a counterexample:

this is an existence proof by explicit construction. the claim “model weights cannot contain copies” requires that no model ever contains copies. i’ve falsified this claim through a single counterexample (trivial though it may be).

i constructed thousands of specific examples where:

• GPL-2.0 licensed code enters as training data
• MIT-licensed weights come out
• GPL-2.0 licensed code comes back out through prompting

the absurdity is self-evident: GPL-2 in, MIT out, GPL-2 back out. if this isn’t license laundering, what is? the weights enable extraction of the original GPL code “with the aid of a machine”—the statutory definition of a copy under 17 U.S.C. §101.

this demonstrates [IV] above: practically all models reproduce some verbatim copies of input data. the Linux demonstration provides explicit construction. i didn’t argue about prevalence or representativeness; i demonstrated that the capability exists. opponents can’t claim “it’s impossible”; i’ve done it. the debate shifts to frequency, mitigation, and legal consequences.

the OSI’s deafening silence

when i posted this demonstration to the Open Source Initiative’s discussion forum in June 2024, asking whether MIT-licensed weights that trivially emit GPL code satisfy their Open Source AI Definition, the response was silence. zero substantive engagement. i drew an analogy to software dependencies: “We would never support a standard that openly ignored transitive dependencies in software.” the open source community has fought for decades to ensure license obligations flow through dependencies, yet when confronted with training data as a dependency, the discussion died.

i followed up a week later, noting that GPT-4o could replicate GPL2 code through low-temperature sampling. still nothing. the models remain fully compliant with the official OSAID v1.0 (and were compliant with draft 0.0.8 at the time of discussion) despite demonstrably containing extractable GPL code. the cognitive dissonance is striking: we treat software dependencies with rigorous license tracking, but when the same GPL code passes through neural network compression, it somehow becomes exempt.

we’ve now demonstrated that models can produce exact copies of training data. but copyright concerns extend beyond verbatim reproduction. even when models don’t copy perfectly, they can create functional substitutes that serve the same purpose as the original work. in near copies and substitution: why factor 4 fails for generative ai, we examine how models create market-harming outputs through functional equivalence, even without perfect copying.

having established that models can and do emit verbatim copies, we now return to the formal mathematical claim made by courts and show it false.

[V] the formal proof: model weights contain copies

we now arrive at the climax of our argument. everything established in I-IV builds to this: a formal mathematical proof that the judicial claim “model weights do not contain copies” is false.

the claim

when courts state that a model “does not store or reproduce any copyright works,” they’re making a precise claim about what the model contains:

• training data = all sequences in the dataset used to train the model
• extractable sequences = all sequences that can be extracted from the model weights using prompts

the judicial claim translates to:

“model weights contain zero copies of training data”

that is, no training sequences can be extracted from the model. zero overlap. no copies.

the legal basis

this framing matters because copyright law defines “copy” broadly.

under 17 U.S.C. §101, a “copy” is any material object in which a work is fixed “by any method now known or later developed, and from which the work can be perceived, reproduced, or otherwise communicated, either directly or with the aid of a machine or device.”

the UK’s Copyright, Designs and Patents Act 1988 (CDPA) §17 similarly defines reproduction to include storage “in any medium by electronic means.”

courts have long held that human-readability is not required:

• MAI Systems Corp. v. Peak Computer (9th Cir. 1993): loading software into RAM (where it exists only as electrical charges) creates a copy
• Apple Computer v. Franklin (3d Cir. 1983): object code (machine-readable binary) is a copy of the underlying source code

the critical phrase: “with the aid of a machine or device.”

if a training sequence can be extracted from model weights using a prompt (a machine-aided process), then the model contains a “copy” of that sequence under the plain statutory language.

the proof

this is a falsifiable claim. we don’t need to measure degrees of similarity or argue about what “counts” as copying. we only need to demonstrate that at least one training sequence can be extracted verbatim from the model.

from section [IV], i demonstrated explicit construction:

• trained models on Linux kernel v1.0 source code
• extracted GPL-licensed file contents verbatim from the trained model
• showed the extracted sequences are identical to training data

i constructed thousands of specific examples (GPL file contents) where they’re in the training data, can be extracted with prompts, and therefore exist as verbatim copies in the weights.

but the claim doesn’t just fail for toy models—it fails for production language models from leading AI companies:

• Carlini et al. (2021) extracted verbatim training data from GPT-2, including complete licenses, personal information, and long copyrighted passages. they demonstrated that a commercial model from OpenAI stores retrievable copies of training sequences.

• Brown et al. (2020), OpenAI’s own GPT-3 paper, documented 13-gram overlap with evaluation benchmarks—memorization so extensive that OpenAI had to redo evaluations. this admission came from the model’s creators, not external researchers.

• Patronus AI (2024) tested leading models and found GPT-4 produced copyrighted content on 44% of adversarial prompts, including 161-word passages from Harry Potter. a commercial, RLHF-aligned model still emits verbatim copyrighted sequences.

• Cooper et al. (2025) found that Llama 3.1 70B completely retained copyrighted novels. researchers could “deterministically generate the entire book near-verbatim” for Harry Potter and the Philosopher’s Stone. an entire novel, extractable on demand.

the Linux demonstration was an existence proof by construction: i showed it’s possible in principle. these papers demonstrate it happens in practice across GPT-2, GPT-3, GPT-4, and Llama—models serving hundreds of millions of users.

conclusion: the claim “model weights contain zero copies” is proven false for toy models (my construction) and proven false for production models (OpenAI, Meta). the judicial claim fails as an empirical matter.

legal implications

if compressing GPL-2.0 kernel source into model weights allows relicensing under MIT, then by the same logic:

• can i compress a GPL library into a .tgz file and relicense it as Apache 2.0?
• can i encrypt GPL code with AES and claim it’s now proprietary?
• can i encode it in base64 and ignore copyleft obligations?

the answer to all of these is “no.”

the reason: in all cases, the compressed artifact is one from which the original can be extracted “with the aid of a machine.” the .tgz file, the encrypted file, the base64 string—all allow extraction of the original work with appropriate tools. if the original can be extracted, the compressed form is a “copy” under statutory language. importantly, some architectures and training regimes do reduce output-time verbatim copying (e.g., encoder-only models, aggressive deduplication, stronger regularization, or alignment), but that mitigation does not resolve whether copies existed at earlier stages (dataset assembly) or whether weights fix extractable sequences for a subset of content.

neural network weights are no different. the evidence above—from my Linux demonstration, Carlini’s GPT-2 extractions, OpenAI’s GPT-3 admissions, Patronus’s GPT-4 testing, and Stanford’s Llama analysis—establishes that training sequences can be extracted from model weights using prompts. this isn’t theoretical. it’s documented across model architectures, company boundaries, and alignment techniques.

the form doesn’t matter. compressing a novel into a .gz file, encrypting a screenplay with AES, or encoding GPL source code in neural network parameters—all create “copies” if the work can be perceived or reproduced with technological assistance.

this proves [V] above: for sufficiently complex sequences, any device that can create an indistinguishable copy must encode that information. model weights allow extraction of training data (proved in [IV]), therefore the weights contain copies under the statutory language “with the aid of a machine or device.” the proof is an existence claim: models contain copies of at least some training sequences.

the three legal questions

current litigation involves three distinct questions:

question 1: copying to assemble training datasets is it infringement to scrape copyrighted works and compile them into training datasets?

• US: likely fair use if transformative
• UK: requires TDM exception or license
• EU: permitted under TDM exceptions with opt-out

question 2: copies in model weights do trained model weights constitute copies or derivative works of training data?

• UK Getty: no—weights don’t “store or reproduce” works ([2025] EWHC 2863 (Ch))
• US Andersen: plausible theory allowed past pleadings (No. 3:23-cv-00201)
• our demonstration: addresses this directly—weights contain extractable copies of training data

question 3: copying in model outputs if a model outputs verbatim or substantially similar training data, is that infringement?

• largely unresolved in case law
• likely yes for substantial verbatim reproduction
• uncertain for stylistic similarity or paraphrase

our technical argument directly answers question 2: the capacity evidence and Linux demonstration show weights do contain compressed representations extractable “with the aid of a machine.” note also that question 1 (dataset assembly) concerns a distinct reproduction event—often defended under fair use (US) or TDM exceptions (EU and some member states). even where output-time verbatim copying is mitigated by architecture/regularization/alignment, the legality of the initial copying and the fixation of information in weights remain separate analyses with potentially different defenses and outcomes.

this post has focused on question 2: whether weights contain copies. we’ve shown they do. for question 3—whether model outputs infringe through near-copying and create market harm—see near copies and substitution: why factor 4 fails for generative ai. that post examines how substitution capability affects fair use analysis, particularly factor 4 (market harm).

having shown that weights contain copies, we now assess what this post has established.

what we’ve established vs. what requires study

the strength of any scientific claim rests on clarity about its scope. we can demonstrate technical capabilities. we cannot demonstrate economic behavior without behavioral data. conflating the two weakens both science and policy. here’s what the evidence in sections I-IV and VI actually establishes, what it doesn’t, and why the distinction matters for litigation.

established with evidence (what this post demonstrates)

✅ information-theoretic foundations: the connection between compression and copying is mathematically formal. Cover & Thomas prove that minimizing cross-entropy is equivalent to minimizing code length. Rissanen’s MDL principle shows that models minimize total description length. mathematical equivalence, not analogy.

✅ theoretical necessity of memorization: Feldman proved that for long-tail distributions (like natural language), memorization of rare sequences is mathematically necessary to achieve low generalization error. not a bug to engineer away. it’s designed into the learning objective.

✅ mechanisms are understood: sections I-III showed that memorization isn’t mysterious. it follows from capacity constraints (Morris et al. 3.6 bits/parameter), duplication frequency (Biderman et al. Pythia study), and training dynamics (learning rate schedules, data ordering). we can predict which sequences get memorized.

✅ verbatim extraction exists: section IV demonstrated that models contain and can emit exact copies of training data, proved through explicit construction with the Linux kernel models and documented in peer-reviewed research (Carlini, Cooper, etc.).

what this post doesn’t address: whether models create market-harming substitutes, how courts should weigh empirical evidence gaps, and factor 4 analysis. those questions are examined in near copies and substitution: why factor 4 fails for generative ai.

architectural and jurisdictional variations (degree, not kind)

one legitimate response to sections I-IV and VI is: “but not all models behave this way.” true. let’s be precise about variations.

architectural differences do affect degree:

• encoder-only models (BERT, RoBERTa): masked language modeling instead of autoregressive generation. Diera et al. (2023) showed they still memorize named entities, but they’re more resistant to extraction attacks than GPT-style models. the capability remains; extraction difficulty increases.
• deduplication reduces memorization: Biderman et al. demonstrated this with Pythia deduplicated variants. repeated sequences memorize less. but unique outliers and sequences with moderate duplication still get memorized. it’s risk reduction, not elimination.
• alignment suppresses verbatim: RLHF and DPO can reduce unintended memorization by penalizing verbatim training data reproduction. Su et al. (2024) showed this mitigation works but isn’t perfect. targeted attacks still extract memorized content.

these variations matter for section IV and VI claims: they affect how much content is extractable and under what conditions. but they don’t negate the existence claim. even if only 0.1% of outputs contain verbatim training data (GPT-2 rate), that’s still thousands of extractable sequences in a large model. the judicial claim “weights contain zero copies” remains false.

jurisdictional variations matter for section VII market harm:

• US: broad transformative use doctrine. courts weigh all four factors but emphasize transformation. plaintiffs need strong market harm evidence to overcome transformative use findings.
• UK: narrower fair dealing. no broad transformative use exception. text and data mining (TDM) exception exists but doesn’t resolve output infringement. Getty decision focused on whether weights “store” works, not market impact.
• EU: mandatory TDM exceptions but with opt-out rights. rights holders can prevent training use. output infringement and market harm remain separate questions under national laws.

these jurisdictional differences affect legal outcomes but don’t change the technical facts in sections I-VI. memorization mechanisms work the same way in US, UK, and EU models. what changes is the legal framework applied to identical technical behavior.

the honest assessment

what this post has accomplished:

• established information-theoretic foundations (Cover & Thomas, MDL)
• proved theoretical necessity of memorization (Feldman)
• demonstrated models compress training data (I-II)
• showed memorization is predictable and measurable (III)
• demonstrated verbatim extraction exists (IV, VI)

what this post hasn’t established:

• that substitution occurs at economically significant scale (see near copies and substitution: why factor 4 fails for generative ai)
• that markets have measurably shifted due to AI-generated substitutes (see near copies and substitution: why factor 4 fails for generative ai)
• that users intend to avoid paying for originals when using models (see near copies and substitution: why factor 4 fails for generative ai)
• that fair use analysis should resolve differently than recent US court decisions

why this matters: fair use is a mixed question of law and fact. the legal framework (transformative use, market effect) is settled doctrine. what’s missing is factual development: economic studies, user surveys, market data. capability arguments (what we’ve established) show that harm is possible. but courts weigh actual harm, not hypothetical harm. without empirical evidence, the fourth factor becomes a default win for whoever argues most persuasively about analogies.

this post demonstrates that the technical capability for market-harming substitution exists, that memorization is systematic and measurable, and that current judicial claims about compression and copying are incorrect as statements of technical fact. but it’s intellectually honest to admit: proving capability isn’t proving behavior. the next phase requires economists, not computer scientists.

having clarified what we’ve established and what we haven’t, we should address the strongest counterarguments.

counterarguments: steel-manning the other side

to be fair, there are legitimate arguments on the other side of this debate. let me present them as charitably as possible before explaining why the technical evidence still matters.

argument 1: weights aren’t copies, outputs might be

some courts and legal scholars argue that model weights themselves aren’t “copies” of training data; they’re learned statistical representations. under this view, any infringement occurs at output time, when the model generates text that reproduces protected works. the UK Getty court essentially took this position: the model doesn’t “store or reproduce” works, even though specific outputs might.

argument 2: training is transformative use

US courts in Bartz v. Anthropic and Kadrey v. Meta found AI training to be “spectacularly transformative”: the model isn’t reading works for their expressive content but extracting statistical patterns. this is analogous to Google Books scanning millions of books to enable search, which was held to be fair use.

supporters cite Authors Guild v. Google Inc., 804 F.3d 202 (2d Cir. 2015), where scanning millions of books to enable search was transformative fair use. they also point to Kelly v. Arriba Soft Corp., 336 F.3d 811 (9th Cir. 2003), where thumbnail images in search results were transformative despite being exact copies at lower resolution—the original purpose was aesthetic, while the search engine purpose was indexing and access. as the court noted, the “use did not supplant need for originals” and “benefitted public by enhancing Internet information gathering.”

argument 3: TDM exceptions permit training

the EU’s text and data mining (TDM) exceptions and similar research carve-outs in various jurisdictions explicitly permit making copies for computational analysis. the German Kneschke v. LAION decision applied this logic: copying for dataset creation and research is permitted even if it involves making intermediate copies.

argument 4: outputs are the only actionable harm

from a policy perspective, if models rarely produce verbatim training data (0.1-1% under targeted prompting), perhaps the law should focus on output liability rather than the training process. this allows innovation while still protecting creators from direct substitution.

argument 5: substantial noninfringing uses

Sony Corp. of America v. Universal City Studios, Inc. (the Betamax case), 464 U.S. 417 (1984) established that sale of copying equipment doesn’t constitute contributory infringement if the product is “widely used for legitimate purposes” and has “substantial noninfringing uses.” VCRs could be used for both infringing copying and time-shifting (which the Court found to be fair use). defenders argue that AI models similarly have substantial noninfringing uses: generating original content, assisting creativity, answering questions based on general knowledge. the capability to memorize some training data doesn’t make the entire system infringing if most uses are legitimate.

argument 6: intermediate copying for transformative purposes

Sega Enterprises Ltd. v. Accolade, Inc., 977 F.2d 1510 (9th Cir. 1992) held that intermediate copying during reverse engineering is fair use “where reverse engineering is the only means of gaining access to unprotected aspects of the program” and there’s a legitimate reason. disassembly of object code was permitted when necessary to access unprotected elements. by analogy, training might constitute “intermediate copying” for the transformative purpose of extracting statistical patterns, even if copyrighted works are copied in the process.

argument 7: constitutional purpose promotes progress

Google LLC v. Oracle America, Inc., 593 U.S. 1 (2021) held that Google’s copying of 11,500 lines of Java API code (~0.4% of the program) to make Android compatible was transformative fair use. critically, the Court emphasized that “to allow enforcement of copyright here would risk harm to the public” in promoting science and useful arts—the Constitutional purpose of copyright. the declaring code “derived value from programmers who learned it.” defenders argue that blocking AI training would similarly harm the public interest in technological progress and that training data similarly derives value from the community of users and creators who contributed to it.

argument 8: the fixation doctrine challenge (cablevision)

this is potentially the most devastating counterargument to the “weights contain copies” theory. Cartoon Network LP, LLLP v. CSC Holdings, Inc. (Cablevision), 536 F.3d 121 (2d Cir. 2008) held that temporary buffer copies (lasting only 1.2 seconds) were NOT “fixed” under the Copyright Act because they weren’t perceivable “for a period of more than transitory duration.” fixation requires embodiment that permits perception by others.

applied to neural networks: model weights don’t contain perceivable works in any straightforward sense. the copyrighted text, images, or code only appears after inference—a separate computational act performed by users at a later time. before inference, the weights are just billions of floating-point numbers with no recognizable content. if 1.2-second buffer copies aren’t “fixed” because they’re transitory, how can weights that require complex matrix operations to reconstruct content constitute fixation?

this argument goes directly to whether weights constitute “copies” at all. if accepted, it would mean: (1) the copying happens at dataset assembly (potentially defensible under TDM exceptions or transformative use), and (2) any infringement occurs at output time when users generate infringing content (a separate act of direct infringement by users, not by model developers). this would fundamentally reshape liability theory from “weights contain infringing copies” to “outputs may infringe but weights don’t.”

my rebuttal: the proof in [V] is decisive

these arguments have merit as policy positions, but they don’t account for the mathematical reality:

1. statutory definition of “copy” explicitly includes fixations perceivable “with the aid of a machine.” our proof in [V] shows thousands of training sequences can be extracted from weights. the weights contain copies under plain statutory language.

2. the cablevision fixation challenge (argument 8) deserves serious engagement. it’s the strongest technical-legal counterargument. my response: the distinction between cablevision’s 1.2-second buffer and model weights is permanence and intent. cablevision’s buffer was designed to be ephemeral—data flowed through transiently with no persistent storage. model weights are designed to be permanent: stored on disk, versioned, distributed, and used repeatedly over months or years. the “transitory duration” standard doesn’t apply to persistent storage media. moreover, cablevision focused on whether intermediate technical copies (created as a side effect of transmission) constitute fixation. model weights aren’t transmission buffers—they’re the product. their entire purpose is to encode information for later retrieval. that’s fixation by design, not transitoriness.

   however, i acknowledge this argument has real force. if courts accept that weights don’t “contain” works because reconstruction requires inference (a separate act), then the “weights are copies” theory fails. plaintiffs would need to pursue alternative theories: dataset assembly infringement, contributory infringement (providing tools that enable user infringement), or focusing solely on output liability. this is a vulnerability in [V]‘s legal reasoning that requires careful analysis by courts.

3. selective memorization is systemic, not rare. duplicated content (licenses, boilerplate, famous texts) is memorized at very high rates. the 0.1-1% figure measures rare extraction events, but what matters legally is whether models contain any copies, which we’ve proven mathematically.

4. the Linux demonstration provides explicit construction. we demonstrated specific verbatim sequences—that’s a proof by counterexample. the judicial claim “no copies exist” is falsified, not debatable. even if cablevision’s fixation doctrine creates ambiguity about when copying occurs, it doesn’t eliminate that copying happens somewhere in the pipeline.

5. TDM exceptions typically distinguish between copying to train and copying in the resulting artifact. even if assembling training data is permitted, the claim “weights contain no copies” is an empirical question, not a legal presumption. we’ve proven it’s false (subject to the cablevision challenge).

6. substantial noninfringing uses (argument 5, sony betamax) is a contributory infringement defense, not a fair use defense. even if models can generate original content, if they also enable systematic reproduction of training data, the betamax standard may not apply. importantly, betamax concerned time-shifting of broadcasts users were already entitled to watch—it didn’t create new access to copyrighted works. AI models enable access to training data that users never licensed. the analogy is imperfect.

7. google v. oracle’s constitutional argument (argument 7) cuts both ways. yes, copyright serves progress. but so does compensating creators whose works enable that progress. oracle lost because APIs are functional interfaces with network effects—blocking reimplementation would create monopoly lock-in contrary to constitutional purposes. training data isn’t functional interface code; it’s creative expression. the constitutional balance arguably favors creators whose works are being used without compensation, especially when licensing markets exist.

8. sega’s intermediate copying (argument 6) applied to reverse engineering for interoperability—accessing unprotected functional elements. courts have narrowly construed this exception. AI training isn’t accessing “unprotected elements” (like game console compatibility requirements); it’s extracting patterns from protected creative expression. the analogy is strained.

the technical evidence doesn’t resolve the policy question of what the law should be. we can debate whether arguments 1-7 should govern. but the claim “model weights do not contain copies” is mathematically false (subject to cablevision’s fixation challenge, which reframes when/where copying occurs). [I] through [VI] are established facts about technical capability. courts must start from accurate technical premises—and must grapple with whether cablevision’s transitory duration standard applies to permanent storage of compressed information.

note: this concludes “model weights contain copies: compression is not magic.” in a companion post, near copies and substitution: why factor 4 fails for generative ai, we examine how ai models create functional substitutes that harm markets even when they don’t produce verbatim copies—and why this substitution capability defeats fair use defenses under factor 4 analysis.

conclusion: compression is not magic

arthur c. clarke wrote that sufficiently advanced technology is indistinguishable from magic. he didn’t mean it escapes physical laws—only that its workings aren’t obvious to observers. recent judicial opinions sometimes treat neural network compression this way, as if complexity creates exemption.

it doesn’t. the Linux demonstration shows the absurdity: GPL kernel source enters training, MIT-licensed weights emerge, GPL code exits through prompting. if the weights don’t “contain” the sequences required to emit that code, the word “contain” has no meaning. the statutory definition is explicit—works fixed in material form “from which the work can be perceived, reproduced, or otherwise communicated, either directly or with the aid of a machine”—and we’ve satisfied it thousands of times over. no interpretive gymnastics, just plain application of the text.

Feldman’s proof closes the engineering escape hatch. for long-tail distributions like natural language, memorization of rare sequences isn’t overflow from careless capacity planning—it’s mathematically necessary for achieving low generalization error. you can’t “denoise” away the GPL license or the copyrighted novel excerpt because compression-optimal solutions store them. claiming better practices will eliminate memorization is claiming you can violate information theory.

what changes if courts accept this? question 2 from section VI—whether weights contain copies—gets resolved against “no copies exist” claims. question 1 (dataset assembly) and question 3 (output infringement) remain live, with their own defenses and analyses. but the “weights are just statistical patterns with no fixation” theory collapses. if compressed encodings aren’t copies when extractable by machine, then neither are .zip files, encrypted backups, or base64 strings. copyright law doesn’t distinguish based on compression sophistication.

the economic question—whether models create market-harming substitutes even without verbatim output—we examine in near copies and substitution: why factor 4 fails for generative ai. that post argues capability for substitution creates market harm under factor 4, the decisive fair use factor.

compression isn’t magic. it’s mathematics you can measure. where legal claims deny what measurements show, we call out the conflict. when courts state “model weights do not contain copies,” they’re making an empirically falsifiable claim. we’ve falsified it.

ps: this analysis builds on extensive research from EleutherAI, OpenAI, Google DeepMind, Meta, and others who have rigorously studied memorization in language models. the ChatGPT research scaffold that informed parts of this post provides comprehensive citations and legal context. special credit in particular to Stella Biderman and the EleutherAI team for their pioneering work on memorization through Pythia, the first open model family that allowed researchers to independently examine these phenomena.

references

academic papers

foundations: information theory and mdl:

• Shannon, Claude E. “A Mathematical Theory of Communication.” Bell System Technical Journal 27 (1948): 379–423, 623–656. doi
• Cover, Thomas M., and Joy A. Thomas. Elements of Information Theory, 2nd ed. Wiley, 2006. book
• Rissanen, Jorma. “Modeling by Shortest Data Description.” Automatica 14, no. 5 (1978): 465–471. doi
• Li, Ming, and Paul Vitányi. An Introduction to Kolmogorov Complexity and Its Applications, 4th ed. Springer, 2019. book

compression and language modeling:

• Delétang, Grégoire, et al. “Language Modeling Is Compression.” arXiv:2309.10668, 2023. paper
• Wang, Peng, et al. “Understanding Deep Representation Learning via Layerwise Feature Compression and Discrimination.” arXiv:2311.02960, 2023. paper

tokenization and subword units:

• Gage, Philip. “A New Algorithm for Data Compression (Byte Pair Encoding).” C Users Journal, Feb 1994. article
• Sennrich, Rico, Barry Haddow, and Alexandra Birch. “Neural Machine Translation of Rare Words with Subword Units.” arXiv:1508.07909, 2015. paper

memorization studies:

• Biderman, Stella, et al. “Emergent and Predictable Memorization in Large Language Models.” arXiv:2304.11158, 2023. paper
• Brown, Tom, et al. “Language Models are Few-Shot Learners.” arXiv:2005.14165, 2020. paper (GPT-3 paper)
• Carlini, Nicholas, et al. “Extracting Training Data from Large Language Models.” 30th USENIX Security Symposium, 2021. paper
• Feldman, Vitaly. “Does Learning Require Memorization? A Short Tale about a Long Tail.” STOC 2020, arXiv:1906.05271, 2020. paper
• Feldman, Vitaly, and Chiyuan Zhang. “What Neural Networks Memorize and Why: Discovering the Long Tail via Influence Estimation.” NeurIPS 2020, arXiv:2008.03703, 2020. paper
• Cooper, A. Feder, Aaron Gokaslan, Ahmed Ahmed, Amy B. Cyphert, Christopher De Sa, Mark A. Lemley, Daniel E. Ho, and Percy Liang. “Extracting memorized pieces of (copyrighted) books from open-weight language models.” arXiv:2505.12546, 2025. paper
• Dana, Lior, Manish Suresh Pydi, and Yann Chevaleyre. “Memorization in Attention-only Transformers.” arXiv:2411.10115, 2024. paper
• Diera, Agnes, Nils Lell, Alisa Garifullina, and Ansgar Scherp. “Memorization of Named Entities in Fine-tuned BERT Models.” CD-MAKE 2023, arXiv:2212.03749, 2023. paper
• Mahdavi, Sadegh, Renjie Liao, and Christos Thrampoulidis. “Memorization Capacity of Multi-Head Attention in Transformers.” ICLR 2024, arXiv:2306.02010, 2024. paper
• Meeus, Matthijs, et al. “Recite, Reconstruct, Recollect: Memorization in LMs as a Multifaceted Phenomenon.” arXiv:2406.17746, 2024. paper (copyright traps paper)
• Meeus, Matthieu, Igor Shilov, Manuel Faysse, and Yves-Alexandre de Montjoye. “Copyright Traps for Large Language Models.” ICML 2024, PMLR 235:35296–35309, arXiv:2402.09363, 2024. paper
• Shilov, Igor, Matthieu Meeus, and Yves-Alexandre de Montjoye. “Mosaic Memory: Fuzzy Duplication in Copyright Traps for Large Language Models.” arXiv:2405.15523, 2024. paper
• Morris, John X., Chawin Sitawarin, Chuan Guo, Narine Kokhlikyan, G. Edward Suh, Alexander M. Rush, Kamalika Chaudhuri, and Saeed Mahloujifar. “How much do language models memorize?” arXiv:2505.24832, 2025. paper
• Patronus AI. “Introducing CopyrightCatcher, the first Copyright Detection API for LLMs.” March 2024. announcement
• Wallace, Eric, et al. “Does GPT-2 Know Your Phone Number?” BAIR Blog, Dec 2020. post
• Wei, Jiaheng, et al. “Memorization in deep learning: A survey.” arXiv:2406.03880, 2024. paper

dataset deduplication and contamination:

• Lee, Katherine, Daphne Ippolito, Andrew Nystrom, Chiyuan Zhang, Douglas Eck, Chris Callison-Burch, and Nicholas Carlini. “Deduplicating Training Data Makes Language Models Better.” arXiv:2107.06499, 2021. paper

model capacity and scaling:

• Hoffmann, Jordan, et al. “Training Compute-Optimal Large Language Models.” arXiv:2203.15556, 2022. paper (Chinchilla paper)
• Kaplan, Jared, et al. “Scaling Laws for Neural Language Models.” arXiv:2001.08361, 2020. paper

training and optimization:

• Loshchilov, Ilya, and Frank Hutter. “Decoupled Weight Decay Regularization.” ICLR 2019, arXiv:1711.05101, 2019. paper (AdamW)
• Rafailov, Rafael, et al. “Direct Preference Optimization: Your Language Model is Secretly a Reward Model.” arXiv:2305.18290, 2023. paper (DPO)
• Ruan, Zhihao, et al. “Unveiling Over-Memorization in Finetuning LLMs for Reasoning Tasks.” arXiv:2508.04117, 2025. paper
• Schulman, John, et al. “Proximal Policy Optimization Algorithms.” arXiv:1707.06347, 2017. paper (PPO)
• Su, Edwin, et al. “Extracting Memorized Training Data via Decomposition.” arXiv:2409.12367, 2024. paper

training data extraction and attacks (language models):

• Nasr, Milad, Nicholas Carlini, Jonathan Hayase, Matthew Jagielski, A. Feder Cooper, Daphne Ippolito, Christopher A. Choquette-Choo, Eric Wallace, Florian Tramèr, and Katherine Lee. “Scalable Extraction of Training Data from (Production) Language Models.” arXiv:2311.17035, 2023. paper

memorization and extraction (diffusion/image models):

• Carlini, Nicholas, Jamie Hayes, Milad Nasr, Matthew Jagielski, Vikash Sehwag, Florian Tramèr, Borja Balle, Daphne Ippolito, and Eric Wallace. “Extracting Training Data from Diffusion Models.” USENIX Security 2023, arXiv:2301.13188, 2023. paper
• Chen, Chuxiao, Ximing Lu, Yizhou Zhou, Shuohang Wang, Yang Song, Yash Sharma, and Kilian Q. Weinberger. “Exploring Local Memorization in Diffusion Models via Bright Ending Attention.” ICLR 2025 Spotlight, arXiv:2410.21665, 2024. paper github
• Chen, Yunhao, Xingjun Ma, Difan Zou, and Yu-Gang Jiang. “Extracting Training Data from Unconditional Diffusion Models.” arXiv:2406.12752, 2024. paper
• Wang, Wenhao, Yifan Sun, Zhentao Tan, and Yi Yang. “Image Copy Detection for Diffusion Models.” NeurIPS 2024, arXiv:2409.19952, 2024. paper
• Wang, Zhe, Yuchen Liu, Yubei Chen, Yangyang Wang, Jia Wang, and Jianye Hao. “Could It Be Generated? Towards Practical Analysis of Memorization in Text-To-Image Diffusion Models.” arXiv:2405.05846, 2024. paper
• Webster, Ryan. “A Reproducible Extraction of Training Images from Diffusion Models.” arXiv:2305.08694, 2023. paper
• Wen, Yuxin, John Kirchenbauer, Jonas Geiping, and Tom Goldstein. “Tree-Rings Watermarks: Invisible Fingerprints for Diffusion Images.” NeurIPS 2023, 2023. paper

memorization and extraction (audio models):

• Bharucha, François G., Mojtaba Heydari, Fengyan Shi, and Yizhou Sun. “Generation or Replication: Auscultating Audio Latent Diffusion Models.” ICASSP 2024, 2024. paper merl
• Epple, Pascal, Igor Shilov, Bozhidar Stevanoski, and Yves-Alexandre de Montjoye. “Watermarking Training Data of Music Generation Models.” arXiv:2412.08549, 2024. paper
• Messina, Francisco, Francesca Ronchini, Luca Comanducci, Paolo Bestagini, and Fabio Antonacci. “Mitigating data replication in text-to-audio generative diffusion models through anti-memorization guidance.” arXiv:2509.14934, 2025. paper

membership inference and privacy:

• Shokri, Reza, Marco Stronati, Congzheng Song, and Vitaly Shmatikov. “Membership Inference Attacks against Machine Learning Models.” arXiv:1610.05820, 2016. paper
• Jagannatha, Abhyuday, Bhanu Pratap Singh Rawat, and Hong Yu. “Membership Inference Attack Susceptibility of Clinical Language Models.” arXiv:2104.08305, 2021. paper

technical resources

• Chawla, Avi. “Gradient Accumulation: Increase Batch Size Without Explicitly Increasing Batch Size.” Daily Dose of Data Science, blog post
• Silva Allende, Alonso. “Next token prediction with GPT.” Hugging Face Blog, Oct 2023. post
• “Byte-Pair Encoding Tokenization.” Hugging Face LLM Course, Chapter 6. tutorial
• Jordan, Keller. modded-nanogpt. GitHub repository, 2025. repo

legal resources

statutes:

• 17 U.S. Code § 107 - Limitations on exclusive rights: Fair use. statute
• “but-for test.” Wex Legal Dictionary, Cornell Law School. definition

cases:

• Andersen v. Stability AI, No. 3:23-cv-00201 (N.D. Cal. 2024)
• Apple Computer, Inc. v. Franklin Computer Corp., 714 F.2d 1240 (3d Cir. 1983)
• Authors Guild v. Google Inc., 804 F.3d 202 (2d Cir. 2015). case
• Bartz v. Anthropic, No. 3:24-cv-05417 (N.D. Cal. Aug. 2024)
• Cartoon Network LP, LLLP v. CSC Holdings, Inc. (Cablevision), 536 F.3d 121 (2d Cir. 2008). case
• Getty Images v. Stability AI, [2025] EWHC 2863 (Ch) (UK High Court, Nov. 2025)
• Google LLC v. Oracle America, Inc., 593 U.S. 1 (2021). opinion
• Kelly v. Arriba Soft Corp., 336 F.3d 811 (9th Cir. 2003). case
• Kneschke v. LAION e.V., Hamburg Regional Court, Case 310 O 227/23 (Sept 2024)
• MAI Systems Corp. v. Peak Computer, Inc., 991 F.2d 511 (9th Cir. 1993)
• Sega Enterprises Ltd. v. Accolade, Inc., 977 F.2d 1510 (9th Cir. 1992). case
• Sony Corp. of America v. Universal City Studios, Inc. (Betamax), 464 U.S. 417 (1984). opinion

secondary sources:

• McIntosh, David M., et al. “A Tale of Three Cases: How Fair Use Is Playing Out in AI Copyright Lawsuits.” Ropes & Gray LLP, July 2025. analysis

project resources

• Linux as a Model (LaaM): 5M model, 32M model, GitHub repository
• Open Source AI Definition: OSAID v1.0 (official release, October 2024); earlier reference to draft 0.0.8 (April 2024)
• OSI Discussion: “GPL2 kernel source as an MIT-licensed model: Is this really open?” forum thread, June 2024
• ChatGPT research scaffold for this post: shared conversation